"The Boundaries of Nature: Special & General Relativity and Quantum Mechanics, A Second Course in Physics:" Edwin F. Taylor's acceptance speech for the 1998 Oersted medal presented by the American Association of Physics Teachers, 6 January 1998
[Reprinted from The American Journal of Physics, Volume 66, Number 5 (May 1998), pages 368-376. Copyright © 1998 American Association of Physics Teachers.]
Edwin F. Taylor
Center for Innovation in Learning, Carnegie Mellon University, Pittsburgh, PA 15213
(Now at 22 Hopkins Road, Arlington, MA 02476-8109, email eftaylor@mit.edu)
CAUTION: Greek letters in the text reproduce as Greek only with Netscape
Navagator 4 and higher and Internet Explorer 3 and higher. (Greek letters
in the equations reproduce correctly for any version of these programs.)
ABSTRACT
Public hunger for relativity and quantum mechanics is insatiable, and we should use it selectively but shamelessly to attract students, most of whom will not become physics majors, but all of whom can experience "deep physics." Science, engineering, and mathematics students, indeed anyone comfortable with calculus, can now delve deeply into special and general relativity and quantum mechanics. Big chunks of general relativity require only calculus if one starts with the metric describing spacetime around Earth or black hole. Expressions for energy and angular momentum follow, along with orbit predictions for particles and light. Feynman's Sum Over Paths quantum theory simply commands the electron: Explore all paths. Students can model this command with the computer, pointing and clicking to tell the electron which paths to explore; wave functions and bound states arise naturally. A second full year course in physics covering special relativity, general relativity, and quantum mechanics would have wide appeal -- and might also lead to significant advancements in upper-level courses for the physics major.
INTRODUCTION
It is easy to feel intimidated by those who have in the past received the Oersted Medal, especially those with whom I have worked closely in the enterprise of physics teaching: Edward M. Purcell, whose graduate school notes on nuclear magnetic resonance I had the pleasure of helping to translate from a course he gave in Germany; Vernet Eaton, the master of demonstration experiments, with whom I began my teaching career at Wesleyan University in Connecticut; A. P. French, one of the true scholars in our profession, who struggled with me to understand and describe quantum mechanics under the leadership of another Oersted Medal winner, Jerrold R. Zacharias, the great entrepreneur of physics curriculum revision; Philip Morrison, whose popular writing has informed us all about a thousand topics and who, with his wife Phyllis, encouraged some of the work described here; John Archibald Wheeler, whose presentation of special relativity in a Princeton freshman class in 1964 brought me close to tears
1
and fixed in me a determination to collaborate with him to develop and write up his insights for the world to enjoy.
2
And, at one remove, John Wheeler's Ph.D. student Richard Feynman, whose thesis led to an introduction to quantum mechanics which now, fifty years later, we can exploit for the benefit of the modern student.
These leaders in physics education have much in common: a fascination with the deep structure of Nature, enthusiasm for envisioning this structure in bold new ways, and absolute integrity in presenting both their vision and their own perplexities to an interested audience. All of us can join this enterprise without reservation or restraint, eliminating the need for anyone to express humility, false or otherwise.
Andy Warhol has said that in the future everyone will have fifteen minutes of fame. Well, this is the future, and you have honored me with twice that allotment. I would like to spend my half hour of fame here today describing the substance and strategy of a proposed course called The Boundaries of Nature, A Second Course in Physics, which harnesses the heritage of Einstein, Wheeler, and Feynman to cover special relativity, general relativity, and quantum mechanics in a full-year course that could follow an introductory physics course. The proposed course covers its three topics deeply, without tensors, without differential equations, without wave formalism -- and definitely without the Schrödinger equation! Indeed, in our treatment of Feynman's quantum mechanics the first equation appears one-third of the way through. Yet the theoreticians among us will admit that Feynman's simple vision of quantum mechanics lies deeper than that of Schrödinger.
Anyone with a mastery of basic calculus and an introductory-physics acquaintance with momentum and energy can now explore the boundaries of Nature. Enthusiastic participants should come out of the woodwork -- both the young and those of us who claim maturity. Most of these will not become physics majors, nor should we want them to. But everyone will be deeply immersed in what physics does best: exploring the boundaries of the universe. Almost every week the Hubble Space Telescope and other observational satellites present us with data and breathtaking pictures of deep significance for our view of the universe. The National Science Foundation and the National Aeronautics and Space Administration continue to provide a multi-billion-dollar infomercial for physics and in particular the view of the universe that rests on Einstein's general theory of relativity. At the other end of the scale of size, reports and glorious pictures from the careening worlds of femtosecond flashes and nanotechnology provide the infomercials for our treatment of quantum mechanics. Square wells? Delayed choice experiments? Tunnel diodes? Single-electron transistors? Atomic "lasers"? All of them are now available for us to use in teaching, actual experiments that often approximate pure cases that we have so irresponsibly invoked for decades.
Here is the plan for this talk: First a brief look at general relativity and quantum mechanics, primarily to highlight how these subjects can be presented with no mathematical formalism beyond calculus. Second, some remarks on the proposed course and its potential benefits for various audiences and for the physics major. Finally, an inspirational conclusion.
GENERAL RELATIVITY
Those of us who are not professionals in general relativity have a fuzzy impression of a mystical, terrifying tangle of equations inhabited by monsters called tensors. I have asked questions about general relativity of several experts in the field. With one exception, every single expert has started answering my question by writing down a tensor. That one exception is John Archibald Wheeler. In our thirty years of collaboration on teaching relativity he never once wrote down a tensor. Never. How is this possible? I believe it is because Wheeler feels that tensors are not fundamental; during our collaboration he disciplined himself to talk only about what lies behind the formalism.
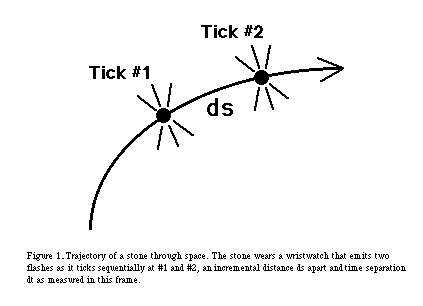
And what does lie behind the formalism of general relativity? Alice's adventure in wonderland begins when a rabbit rushes past her carrying a pocket watch. Our adventure in relativity begins when a stone flies past us wearing a wristwatch (Figure 1)
The wristwatch ticks twice at #1 and #2 (Figure 1). The incremental
3
distance ds and time dt between these ticks, are measured in a particular inertial reference frame. Special relativity warns us that different observers in relative motion may record different values of ds and dt . That is the bad news. The good news is a central finding of special relativity: All inertial observers, whatever their state of relative motion, can calculate the time between ticks d
t
recorded on the stone's wristwatch. The formula is quite simple.
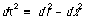 (flat spacetime) (1)
(flat spacetime) (1)
We call d
t
the wristwatch time -- more formally, the spacetime interval -- between these two watch ticks. The quantities ds and dt are values measured directly in any inertial reference frame. For simplicity, the units of space and time are the same, such as light-years and years, or meters of distance and meters of time. Using feet and nanoseconds gives (approximately) similar results.
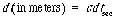 (2)
(2)
Equation (1) that connects the wristwatch time between two adjacent ticks to their coordinate separations is called a metric. The metric tells us the separation between events in spacetime, just as the Pythagorean Theorem tells us the distance between points in Euclidean geometry. The metric is central. Using the metric, it turns out, we can answer every possible (non-quantum) question about spacetime, and with a simple extension we can also predict the trajectories of particles and light.
Now move one step toward general relativity by expressing the metric in polar coordinates in a plane, still describing flat spacetime, spacetime far from stars or planets:
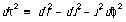 (flat spacetime) (3)
(flat spacetime) (3)
Here dr refers to the increment of the radial distance measured with respect to the center of coordinates and d
f
the small difference in azimuthal angle in the plane.
We enter general relativity
4
by postulating the extension of the metric to a pair of sequential clock ticks that occur on a plane through the center of an uncharged, spherically symmetric, non-rotating massive object. Our study of general relativity begins with this so-called Schwarzschild metric.
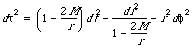 (4)
(4)
Here d
t
is still wristwatch time between two nearby ticks. The new coefficients of dt and dr in the Schwarzschild metric tell us that mass affects spacetime measurements; "Mass tells spacetime how to curve," in Wheeler's phrase. As always in physics, the units of equation (4) need to be carefully defined.
In equation (4) r is the so-called "reduced circumference," derived by measuring the circumference C of a circle centered on the attracting object and then dividing by 2
p
to obtain r = C/(2
p
). The time t is measured on a clock far from the center of attraction. In this brief treatment you have to trust me that such a "far-away time" t can be defined and measured, even for ticks that are not far away from the center of attraction. In a final simplification, mass is measured in units of length:
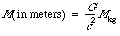 (5)
(5)
Examples:
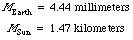 (6)
(6)
Thus does the language of general relativity cut the stars down to size!
Beginning the study of general relativity with the metric, rather than with Einstein's field equations, is the single compromise made in our introductory presentation. The cost of the compromise is significant, namely an inability to analyze time-dependent spacetime phenomena, such as gravitational waves and the formation of stars and black holes. The professional will need to learn about these in a later specialized course. The payoff of the compromise, on the other hand, is prodigious: the ability to analyze in detail and with numerical results many of the classic observations of general relativity using only calculus. Later in the course we provide the Kerr metric for a rotating black hole and draw many fascinating consequences for that case as well.
Do you think that general relativity concerns only events far from common experience? Here is a rough analysis of the timing required for the Global Positioning System (GPS), 24 satellites placed in Earth orbit by the military, which allows any hiker to locate him or herself within a few meters anywhere on Earth. The operation of the Global Positioning System depends crucially on general relativity, specifically on what is loosely and somewhat inaccurately described as the different rates at which clocks run at different distances from a center of gravitational attraction. Here is a quick analysis.
The strategy is to use the far-away time t to relate the wristwatch time between ticks of the satellite clock to the wristwatch time between ticks on the Earth clock.
Both the Earth clock and the satellite clock travel in circular orbits around the center of Earth at constant radius. For this case, dr = 0 for each clock, and we divide the Schwarzschild metric through by the far-away time dt to obtain, for either clock:
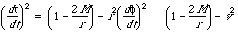 (7)
(7)
We use this equation twice to relate the satellite-clock wristwatch time to the Earth-clock wristwatch time via their common far-away time lapse dt. Write down equation (9) first for the satellite, using r = rsatellite, v = vsatellite, and d
t
= dtsatellite between ticks of the satellite clock, second for the Earth clock, using r = rEarth, v = vEarth and time d
t
= dtEarth between ticks of the Earth clock, for the same lapse dt on the far-away clock. Divide corresponding sides of these two equations to obtain the squared ratio of time lapses recorded on the satellite and earth clocks:
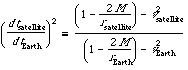 (8)
(8)
A quick calculation shows that the satellite clock runs fast by 38,700 nanoseconds per day compared with the clock on Earth's surface. Light moves about one foot in a nanosecond, so after a single day the Global Positioning System, uncorrected for general relativity, would yield readings in error by many kilometers. Instead, clocks in the orbiting satellites are adjusted to run slow by an amount derived from a more careful calculation. In brief, the Global Positioning System is useless without input from general relativity.
Next I would like to show you the most sophisticated use of mathematics in our whole treatment of general relativity. The following derivation, based on a variational principle, leads to an expression for the energy as a constant of the motion for a stone in orbit around an uncharged, non-rotating, spherically symmetric center of attraction. We can compute particle orbits using this constant energy and a similarly-derived constant angular momentum.
The derivation is based on the twin paradox. Recall that the twin who stays relaxed at home ages more than her identical sister who frantically travels to a distant star and returns. No matter how slowly the traveling twin moves back and forth, or how nearby her destination, her wristwatch always reads less at the reunion than does that of her stay-at-home sister. The lesson of the twin paradox is that the "natural" motion of a free object between two events is the one for which the wristwatch worn by the object has a maximum time reading. Purists insist that we say not maximum reading but extremal reading: either maximum or minimum. We subsume both of these cases under the Principle of Extremal Aging.
Principle of Extremal Aging: The path that an object free of forces takes between two events in spacetime is the path for which the time lapse on its wristwatch is an extremum.
The Principle of Extremal Aging is true also for curved spacetime. It comes naturally and directly out of Einstein's field equations. In our course we simply generalize this Principle from special relativity without derivation.
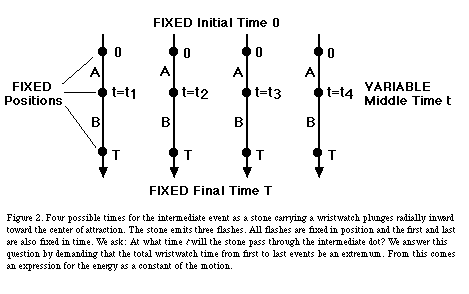
We can use the Principle of Extremal Aging, along with the Schwarzschild metric, to derive an expression for the energy of a particle orbiting a black hole -- or plunging into it. Think of a stone plunging radially toward the center of attraction, as shown in Figure 2. The stone emits three flashes, bracketing two adjacent segments of its trajectory. These segments, A and B in the figure, need not be the same length. We consider all three events to be fixed in space and the first and last events to be fixed in far-away time. Call these first and last times 0 and T. Now we search for the time t at which the stone will pass through the intermediate dot shown in Figure 2.
We use the Principle of Extremal Aging to fix the time t for the intermediate event: The intermediate time t will be such that the stone's wristwatch time from the first to last event is an extremum.
Given time t for the first segment, the elapsed time for segment B is T - t. Let
t
A and
t
B be the wristwatch times for segments A and B recorded by the stone. We are going to take derivatives with respect to the intermediate time t, so we can ignore all terms in the metric that do not contain time. Write two expressions for the metric for these two segments A and B.
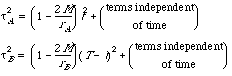 (9)
(9)
Now add the two wristwatch times to yield a total wristwatch time between the first and last events.
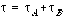 (10)
(10)
Substitute (9) into (10) and take the time derivative of this total wristwatch time with respect to coordinate time t. Set this derivative equal to zero in order to find the time t for which the total wristwatch time
t
is a maximum. After some rearrangement, the result can be written:
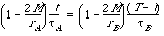 (11)
(11)
The expression on the left side of this equation depends only on the parameters of the first segment A; the expression on the right side depends only on the parameters of the second segment B. Therefore the value of either side must be independent of which segment we choose to look at. We have found a constant of the motion, the same for all segments. Returning to the differential notation, we identify this constant of the motion as the energy, correct for any segment of the path of the plunging particle.
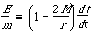 (12)
(12)
Identification with energy E follows by noting that for large r (very far from the center of attraction where spacetime must be flat) the expression reduces to that for energy in special relativity. If you look back over this derivation, you will see that it is equally valid for segments of a non-radial orbit in which the angle
f
changes.
In a similar manner, keeping the time for all three events fixed but varying the angle f of the intermediate event to obtain extremal aging, we derive a second constant of the motion, the angular momentum:
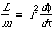 (13)
(13)
Notice that this is almost the same expression as in Newtonian mechanics, with the wristwatch time lapse d
t
replacing the lapse dt in frame time.
The Schwarzschild metric told us that "Mass tells spacetime how to curve." The above expressions for energy and angular momentum complete the handshake between motion and geometry: "Spacetime tells matter how to move." Equations for energy, angular momentum, and the metric give us three equations in the differentials of radius dr, angle d
f,
and time dt. With these we can program a computer to calculate orbits numerically. An expanded analysis includes trajectories of light, which I do not have time to illustrate here.
These and other simple derivations from the metric allow the student to find numerical results for many of the central phenomena of general relativity, including
· energy, angular momentum, and orbits of particles
· precession of Mercury's orbit (without solving differential equations)
· gravitational red shift (previewed in the GPS analysis above)
· orbits of light and deflection of light by Sun (with no geodesic equation)
· gravitational retardation of light
After a few weeks, the student has enough robust tools to tackle such projects as life inside the horizon, pieces of the Friedmann universe, and the properties of spacetime near a rotating black hole -- some of these typically not even part of more advanced courses. In total there are fewer than half a dozen formal integrals in these projects, although the computer is used repeatedly to integrate numerically and to display the outcomes.
So much for general relativity. On to quantum mechanics.
FEYNMAN'S QUANTUM MECHANICS
Physics explores the boundaries of the universe. Two boundaries, the very fast and the very large, are embraced by relativity. Another boundary, the very small, is embraced by quantum mechanics. Most of us envision quantum mechanics as a slippery world of complex wave functions and complex integrals, dominated by the complex Schrödinger partial differential equation.
One day several years ago it dawned on me that the electron is stupid. Or -- so as not to insult any of God's creatures -- let us say that the electron is brainless; no one can argue with that! But we have brains, and surely we can outthink the brainless electron. Ever since that epiphany, my professional life has been guided by the brainlessness of the electron. Faced with a difficulty, one asserts, "This must be simple, because the electron can do it." No obstacle has yet prevailed for long against the surgical slice of that keen blade!
The brainless electron has no chance whatsoever to decode the mysteries of the Schrödinger equation. It requires a simpler set of instructions. Luckily for us, Richard Feynman began to figure this out more than fifty years ago, when he was a Ph. D. student of John Archibald Wheeler at Princeton. (Small world!)
Feynman stands astride the Universe and issues a three-word command so simple that every particle can obey: Explore all paths! Particles are so brainless that they cannot choose a single path, so explore them all. And from this blind exploration come the essential surprises, paradoxes, strangeness -- and power! -- of quantum mechanics. Education research tells us that providing an "organizing principle" for students helps them to understand a subject.
5
Well, here is the organizing principle of the microworld: Explore all paths.
Here are the basic steps in a brief introduction to Feynman's non-relativistic quantum mechanics describing the behavior of an electron:
6
1. The basic command to the electron: Explore all paths!
2. An imaginary stopwatch rotates as the electron explores each path. Earlier our relativistic stone wore a wristwatch. Now Feynman's exploring electron totes a stopwatch.
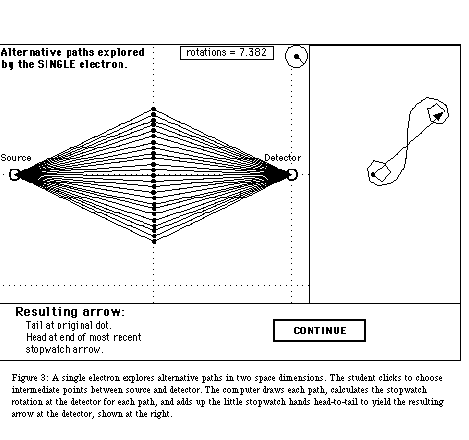
3. The resulting arrow. At the detector, add the little stopwatch hands for all paths head-to-tail to obtain the resulting arrow, sometimes called the quantum amplitude.
4. The probability of detection at that detector is calculated from the squared length of the resulting arrow.
5. Sampling the paths. The student points and clicks on a computer screen to tell the electron which alternative paths to follow between source and detector (Figure 3). This generates a sample of possible paths, not all paths. Nevertheless, a suitable sampling of paths illustrates the basic principles of quantum mechanics.
6. The Principle of Least Action. How much does the electron quantum clock rotate as it explores a given path? To answer this question we digress to examine the Principle of Least Action for the classical description of particle motion. Feynman
7
has a wonderful, eccentric lecture on the subject that treats the trajectory of a stone thrown vertically upward near the surface of Earth. The general expression for the Action along this trajectory is:
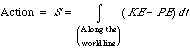 (17)
(17)
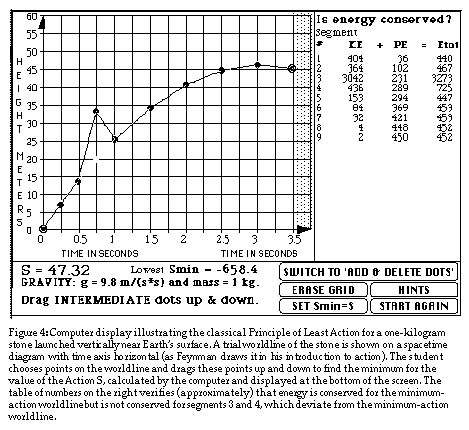
Classical mechanics tells us that the particle will take a path through spacetime for which the Action is an extremum, the so-called Principle of Least Action. We have a piece of software whose display is shown in Figure 4, on which the height of the stone above the ground (vertical axis) is plotted as a function of the time (horizontal axis). We call this a spacetime diagram and give the name worldline to the line on this graph that traces the position of the stone as a function of time. The student places events of launch and catch on the spacetime diagram, then clicks on events intermediate between the two. The computer connects the dots to create a worldline, calculates the value of the Action S for this worldline, and displays this value at the bottom of the screen. The student then drags the intermediate events up and down to minimize the value of the Action S. The result is a parabolic worldline along which the energy is (approximately) conserved. Thus conservation of energy emerges as a natural result of the Principle of Least Action.
Incidentally, equation (17) is the first equation to appear in this treatment of quantum mechanics.
7. Rotation for the hand of the electron quantum clock. Return now to quantum mechanics and notice that we are now talking about worldlines rather than trajectories in space. The generalization of the command to the electron is Explore all worldlines. Non-relativistic quantum mechanics tells us that the number of rotations of the stopwatch hand along a worldline is equal to the value of the Action along that worldline divided by Planck's constant:
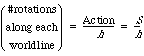 (18)
(18)
This is a basic (underived) postulate of nonrelativistic quantum mechanics.
8. Seamless transition between classical and quantum mechanics. Classical mechanics differs from quantum mechanics in this key respect: in classical mechanics the particle follows a single worldline, whereas in quantum mechanics the particle explores all worldlines. For the quantum case every worldline has an equal vote; it contributes a little stopwatch hand of equal length at the detector. However, most often there exists a minimum-rotation worldline between emission and detection. The cluster of worldlines near to this minimum-rotation worldline contribute their little stopwatch hands more or less in the same direction. The stopwatch hands for worldlines far from this minimum-rotation worldline point in directions radically different from one another and so tend to cancel each other out. The result is an envelope or pencil of worldlines that make the major contribution to the resulting arrow at the detector. As the mass of the particle increases from that of the electron, this pencil of worldlines becomes thinner and thinner. In the limit of large mass, only a single worldline remains -- the worldline predicted by classical mechanics. Thus the transition back and forth between classical and quantum mechanics is seamless in the Sum Over Paths version.
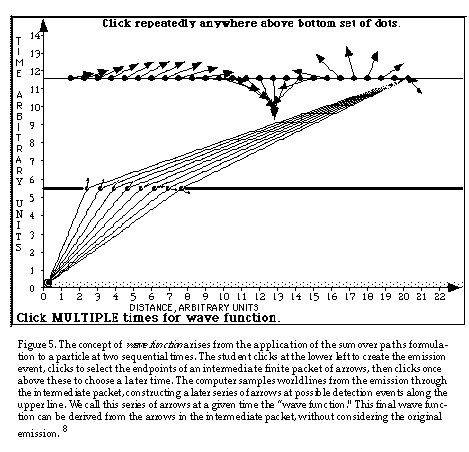
9. The wave function. Next we can graduate from single emission and detection events to initial and final wave functions. Figure 5 shows an intermediate case.
In Figure 5 the time axis is vertical and the space axis horizontal, the professional convention. Here the electron is emitted from a single event, but at a later time we restrict its spatial range to form a packet. Now instead of a single detection event we look at multiple detection events at a single later time. The squared magnitude of each arrow at one of these detection events tells us the relative probability of finding the electron at this place and time. Taken together, this set of arrows is called the wave function.
And now we need no longer be restricted to emission from a single event; instead we start with an initial wave function. The Feynman Sum Over Paths theory then tells us how this initial wave function propagates forward in time, as illustrated in Figure 6.
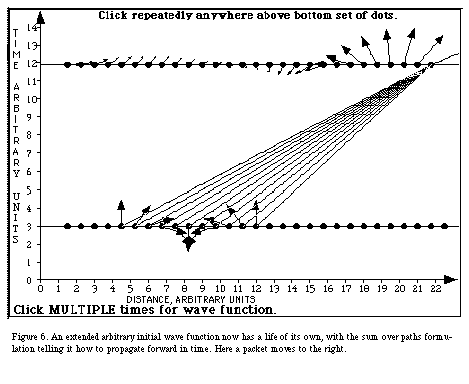
10. The propagator. You may recognize that I have swindled you in various ways in the argument above. In particular, the propagation forward in time shown in Figures 5 and 6 violates the basic command to the electron. In these figures the electron explores only the single, direct worldline from each initial event to each final event in the wave function, not all worldlines as Feynman's command to the electron requires. There is a way to generalize this procedure to take account of all worldlines. It uses a function called the propagator, a function that distills the result of the all-paths exploration between a single initial event and a single final event later in time. The propagator provides the answer to the fundamental question of quantum mechanics, "Given the arrow for a particle at location xa at time ta, what is its arrow at location xb at later time tb?" The propagator is different for different potentials. Given the propagator for a particular potential, you can easily describe the correct development of a wave function through time in that potential. We have developed ways for the student heuristically to "derive" the propagator for a free particle and to employ the known propagator for the simple harmonic oscillator binding potential. I do not have time or space here to describe our derivation and use of propagators, but you can follow the argument in previous publications.
9
Notice that every step in the argument is based simply on electron exploration of alternative worldlines. There is no explicit use of calculus, no explicit complex numbers, no wave formalism, no invocation of phase and group velocities, and no partial differential equations. Yet every feature of one-dimensional complex waves is on display and can be manipulated in preparation for later definitions and formalism.
10
John and Mary Gribbin
11
make a powerful if acerbic case that we have not taken sufficient advantage of Feynman's powerful introduction to both classical and quantum mechanics.
Using Feynman's path integral approach, based on the Principle of Least Action, there is no longer any difference between classical mechanics and quantum mechanics, except for a trivial adjustment to the mathematics. . . . . But this approach never caught on. In universities around the world, even today, half a century after Feynman's insight, students are still taught classical mechanics the old-fashioned way, and then forced to train themselves into a new way of thinking in order to study quantum mechanics using the Hamiltonian approach and the Schrödinger equation. By the time most people learn about Feynman's approach (if they ever do), their brains have been battered by so much mechanics of one kind or another that it is hard to appreciate its simplicity, and galling to realize that they could have saved time and effort by learning quantum theory (and classical theory!) Feynman's way in the first place. Feynman's approach is not the standard way to teach physics for the same reason that the Betamax system is not the standard format for home video, . . . because an inferior system got established in the marketplace first, and continues to dominate as much through inertia and resistance to change as anything else.
These comments are a bit strident, I feel, because Feynman's original Sum Over Paths approach employed difficult mathematical formalism to carry out the summation over all worldlines. But this formalism evaporates as the computer helps our students to sample alternative paths, and I feel we should now pay serious attention to the Gribbins' implicit recommendations for the first and second courses in physics.
THE BOUNDARIES OF NATURE: A SECOND COURSE IN PHYSICS
So we have the components of a full-year course, which I call The Boundaries of Nature: A Second Course in Physics. It follows an introductory physics course and covers special relativity, general relativity, and quantum mechanics. And it covers them deeply. I hope you are now convinced that these subjects can be presented with no mathematical formalism beyond calculus, allowing us to spend our instructional time encouraging intuition and conceptual understanding of non-intuitive situations. Conceptual understanding is necessary so that students (and professionals!) can do order-of-magnitude calculations, guess which aspects of a situation are important and worth modeling, and appreciate the difference between an approximation and an exact calculation. Yet there are plenty of exact calculations in the course. Students are responsible for calculating in detail real results in special and general relativity and for extracting numbers from their manipulation of the software in quantum mechanics.
How far along is the development of teaching materials for these ways of learning special relativity, general relativity, and quantum mechanics?
Special relativity is an old story. The book Wheeler and I wrote on the subject
2
attempts to emphasize the conceptual basis that leads naturally toward general relativity. But there are dozens of different treatments of special relativity: choose your favorite. If you use other introductions, your students may need a briefing on wristwatch time (the spacetime interval) before moving on to general relativity in the Boundaries course, but that is all.
The desktop-published general relativity book,
4
available for the past dozen years, has been used in undergraduate courses in a fair number of schools, lately in several astronomy courses. There is no regular undergraduate course in general relativity, but I believe that the proposed Boundaries of Nature course provides a natural setting for this treatment of general relativity.
And the Feynman Sum Over Paths theory? Our treatment is still evolving as a course. We have developed some software and some student exercises; a couple of papers are in process of publication.
9
Courageous members of this audience are invited to try out our quantum mechanics materials with students and to make their own contributions to their development. Several years of concentrated effort lie ahead before what the students see gleams with the pure light of Feynman's vision.
We have so far neglected a very important component of the Boundaries of Nature course: laboratory. Several groups are working on experiments that might complement our written materials and software programs. I am best acquainted with efforts by Dean Zollman and coworkers.
12
His group has recently described a hands-on activity that helps students visualize motion in potential wells,
13
a central skill in both classical and quantum mechanics. Many relevant experiments can employ light. After all, light is a central player in special and general relativity. Feynman begins his popular treatment of quantum mechanics
14
with photons. Spectra provide us with most of our detailed information about the cosmos precisely because they derive from details of atomic and molecular structure. In addition to laboratories, the Physics Education Group at the University of Washington is developing a series of tutorials based on research into student misunderstandings in relativity.
15
Similar tutorials in quantum mechanics are under development at the Physics Education Research Group at the University of Maryland.
16
No one can be more aware than I am of the incompleteness of our present treatments of general relativity and quantum mechanics. General relativity has a clean story line, but lacks myriad applications to the latest results of astrophysics. Feynman's quantum mechanics is a rich and extensive lode on which we are but early prospectors. We have not yet learned how to teach many applications for which the Sum Over Paths theory will be perfect: barrier penetration, the square well, delayed choice experiments, applications to condensed matter physics. We desperately need help. I look back with nostalgia to a time when Jerrold Zacharias convened world experts to help him start a new curricular project. In one such meeting Zacharias assembled in a single room one Oersted Medal winner (himself) and seven future winners, along with one Nobel Prize winner and one future Nobel Laureate. Is that Age of Giants past? No, I see Giants in front of me today, and recognize several young professionals growing to that stature. Here is a project that challenges our highest skills.
What is the audience for the Boundaries of Nature course? I believe the largest fraction of its class members will not be prospective physics majors, but rather the wide range of students from other sciences, mathematics, and engineering who are comfortable with calculus and hunger for answers to the deep questions that physics engages. One of the most successful general relativity classes has been at Harvard University -- for retirees! The adult population is a vast source of curiosity, commitment -- and money. Our course will enrich their lives as their intellectual and financial presence enriches our colleges and universities.
In my opinion, the Boundaries of Nature course will also have an effect on the upper-level undergraduate program for physics majors. Although the formalism is minimal, the depth of the Boundaries course is phenomenal. Imagine a subsequent junior-year course that treats electricity and magnetism in Lorentz-invariant form. Imagine beginning to study the Schrödinger equation actually knowing where it comes from and what the wave function means. Imagine using spacetime diagrams during the sophomore year, and variational principles then and in later courses. Imagine applying Green's Functions (which is what propagators are) from the beginning of the junior year. Imagine extending the idea of "path" to include Feynman diagrams as part of an undergraduate physics program. Imagine an undergraduate elective in general relativity that calls on tensors and differential forms to buttress and extend an existing understanding of the physical results and to analyze time-dependent phenomena.
How can you learn more about these materials? First, you can examine them yourself.
17
Second, almost every semester I teach an on-line computer conference course on quantum mechanics out of Montana State University, and Nora Thornber teaches similar courses in special relativity (fall semester) and general relativity (spring semester) using our materials.
18
Third, I herewith commit myself to offer workshops in general relativity and quantum mechanics at future AAPT summer and winter meetings as long as I can stand it and as long as the Undergraduate Education Committee continues to sponsor them. But at best these are thin efforts of a small number of people. This lecture and the resulting article plead for the participation of dozens of others in developing and refining their own versions of the Boundaries of Nature course.
It has been almost a hundred years since the wonderful story began, the story of special and general relativity and quantum mechanics. This story is the unique contribution of physics to science and to the history of the world. The larger intellectual community continues to be fascinated by the details and implications of that mighty saga for our everyday lives and for the cosmos. With Einstein, Wheeler, and Feynman at our back, I believe we can now fulfill the implicit but long-delayed promise of our discipline -- to help informed students and professional colleagues explore the Boundaries of Nature and to achieve a really deep understanding of the fundamental workings of our universe.
ACKNOWLEDGMENTS
The treatment of special and general relativity was developed in collaboration with John Archibald Wheeler (references 2 and 4). Special relativity software was developed in collaboration with MIT students and with Paul Horwitz and Kerry Shetline. Some of the treatment of Feynman's Many Paths theory of quantum mechanics was developed with Nora S. Thornber, Stamatis Vokos, and John M. O'Meara (reference 9). Kenneth Johnson, Philip Morrison, and Dan Styer have given encouragement and advice. Current drafts of the quantum mechanics software have benefited fundamentally from advice by David Andersen, Ruth Chabay, and Bruce Sherwood. Specific comments and suggestions on this paper were provided by Ruth Chabay, Paul Horwitz, Priscilla and Ken Laws, Bruce Sherwood, Dan Styer, Nora Thornber, and Stamatis Vokos. And then there is Carla . . .
ENDNOTES:
-
The story of this collaboration is told in Edwin F. Taylor, "The Anatomy of Collaboration, " in Magic without Magic: John Archibald Wheeler, John R. Klauder, editor, W.H. Freeman and Co., New York, 1972.
-
Edwin F. Taylor and John Archibald Wheeler, Spacetime Physics, 2nd Edition 1992, New York, W. H. Freeman Co., ISBN 0-7167-2327-1.
-
By "incremental" we mean that events 1 and 2 are so close together that there is negligible difference between the straight-line distance from one to the other and the length between them measured along the trajectory.
-
E. F. Taylor and J. A. Wheeler, Scouting Black Holes: Exploring General Relativity with Calculus, desktop-published. Available from Taylor: see the website listed in reference 17.
-
Bat-Sheva Eylon and F. Reif, "Effects of Knowledge Organization on Task Performance," Cognition and Instruction, I, 5-44, 1984
-
The following treatment is based loosely on the set of popular lectures: Richard P. Feynman, QED: The Strange Theory of Light and Matter, Princeton University Press, 1985, ISBN 0-691-02417-0. A more advanced treatment is given in R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, New York, McGraw-Hill, Inc., 1965.
-
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Menlo Park 1964, Addison Wesley, Vol. II, Ch. 19.
-
See a similar figure in Feynman and Hibbs, op. cit., Figure 3-3, page 48.
-
E. F. Taylor, S. Vokos, J. M. O'Meara, and N. S. Thornber, "Teaching Feynman's Sum Over Paths Quantum Theory," accepted for publication in the Reviewed Journal Section of Computers in Physics. N. S. Thornber and E. F. Taylor, "Revised Propagator for the Simple Harmonic Oscillator," in process.
-
A. Arons, Teaching Introductory Physics, New York, John Wiley, 1997, pages 234-264.
-
John Gribbin and Mary Gribbin, Richard Feynman, A Life in Science, A Dutton Book, ThePenguin Group, New York, 1997, ISBN 0-525-94124-X, page 89.
-
Consult the Web address http://www.phys.ksu.edu/perg/vqm
-
P. Jolly, D. Zollman, N. S. Rebello, and A. Dimitrova, "Visualizing motion in potential wells," Am. J. Phys., 66, 57-63 (1998).
-
See reference 6.
-
The home page for the Physics Education Group at the University of Washington is http://www-hpcc.astro.washington.edu/scied/physics.html
-
The home page for the Physics Education Research Group at the University of Maryland is http://physics.umd.edu/rgroups/ripe/perg/qm/
-
Taylor's website carries information on latest drafts. http://www.artsaxis.com/eftaylor/
-
For a listing of internet courses, see the World Wide Web location http://www.btc.montana.edu/nten. For a description of our on line courses, see R. C. Smith and E. F. Taylor, "Teaching physics on line," Am. J. Phys., 63, 1090-1096, 1995
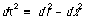 (flat spacetime) (1)
(flat spacetime) (1)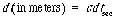 (2)
(2)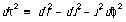 (flat spacetime) (3)
(flat spacetime) (3)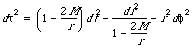 (4)
(4)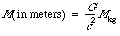 (5)
(5)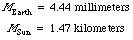 (6)
(6)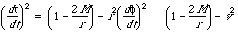 (7)
(7)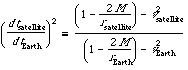 (8)
(8)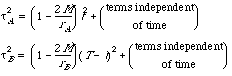 (9)
(9)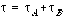 (10)
(10)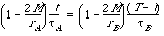 (11)
(11)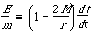 (12)
(12)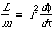 (13)
(13)
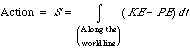 (17)
(17)
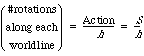 (18)
(18)