American Journal of Physics, Vol. 71, No. 5, pp. 423–425, May 2003
©2003 American Association of Physics Teachers. All rights reserved.
A call to action
Edwin F. Taylor
Department of Physics Massachusetts Institute of Technology Cambridge, Massachusetts 02139
Contents
Would you like to begin the study of Newtonian mechanics using no vectors and no F = ma? How about starting quantum mechanics with no complex numbers and no Schrödinger equation? Would you and your students enjoy exploring general relativity with no tensors and no field equations?
Suppose, further, that along the way your students learn concepts and methods central to contemporary physics research. Finally, what if particle motions described by Newtonian mechanics, general relativity, and quantum mechanics were summarized in three brief but powerful commands of nature that turn out to be variations of the same command?
Physics is already being taught this way, and students respond with enthusiasm and understanding. Moreover, the theoretical background for this curriculum has been around for a long time and is well developed and deeply understood by the physics and mathematics communities.
Here are nature's commands to the stone and electron: At the stone moving with nonrelativistic speed in a region of small space–time curvature, nature shouts: Follow the path of least action!
At the stone moving with any possible speed in a region of any finite space–time curvature, nature shouts: Follow the path of maximal aging!
At the electron, nature shouts: Explore all paths! That's it. We now examine each of these commands in turn.
The principle of least action in Newtonian mechanics1,2 defines the action S for a particle under the influence of a potential: S = ![[integral]](call_action_files/int.gif) L dt =
L dt = ![[integral]](call_action_files/int.gif) (T–V)dt, where T is the kinetic energy, V is the potential energy, and L is the Lagrangian (L = T–V in simple cases) along each segment of the path.3 The quantities T, V, L, and S are scalars. The principle of least action demands that the action S be a minimum for the path taken by the particle.4 For one-dimensional motion in a conservative potential, students can use interactive graphics software to seek out by trial and error the path that minimizes the action.5
(T–V)dt, where T is the kinetic energy, V is the potential energy, and L is the Lagrangian (L = T–V in simple cases) along each segment of the path.3 The quantities T, V, L, and S are scalars. The principle of least action demands that the action S be a minimum for the path taken by the particle.4 For one-dimensional motion in a conservative potential, students can use interactive graphics software to seek out by trial and error the path that minimizes the action.5
The principle of least action appears in Chapter 1 of some advanced texts in classical mechanics.6 By applying the calculus of variations to the action, these texts derive Lagrange's equations, the equations that generalize F = ma. It is not necessary to use the calculus of variations with introductory students; the action is additive, so the principle of least action must apply to each small segment along the path. Therefore elementary calculus suffices to derive Lagrange's equations:7
![(<i>d</i>/<i>d</i><i>t</i>)((([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i>-dot)))–(([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i>)) = 0,](call_action_files/423_1m0.gif)
where q is any independent coordinate, such as the position x or angle 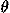 , and
, and 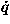 is the time derivative of q. Lagrange's scalar equations allow us to analyze with equal ease the motion of a particle or a system subject to constraints, such as a compound pendulum. In contrast, F = ma requires us to determine every single (vector!) force of constraint before we can describe the motion of even the simplest compound system. As stressed by Max Jammer, "
is the time derivative of q. Lagrange's scalar equations allow us to analyze with equal ease the motion of a particle or a system subject to constraints, such as a compound pendulum. In contrast, F = ma requires us to determine every single (vector!) force of constraint before we can describe the motion of even the simplest compound system. As stressed by Max Jammer, " modern particle physics, just like general relativity, seems to support the thesis that the concept of force has reached the end of its life-cycle—its disbarment from the inventory of fundamental concepts in physics
modern particle physics, just like general relativity, seems to support the thesis that the concept of force has reached the end of its life-cycle—its disbarment from the inventory of fundamental concepts in physics ." 8
." 8
Two criticisms can be leveled against the principle of least action as an introduction to Newtonian mechanics: the concept of action is less concrete and farther from common experience than the concept of force, and the principle of least action and Lagrange's equations deal awkwardly with dissipative and frictional forces. In response to the first criticism, I believe that the comparison should not be between force and action, but rather between vector force and scalar energy. One way to make the concept of action concrete is to introduce it through the conservation of energy. Some introductory texts already begin mechanics with the conservation of energy.9 An analysis of different forms of energy widens the initial scope of the subject and allows discussion of current environmental issues. Early introduction of the potential energy diagram (central to the later study of advanced mechanics, quantum mechanics, and general relativity) permits the qualitative analysis of motion before the use of mathematical formalism.
Then we discover that, given the initial conditions, conservation of energy alone is sufficient to describe completely the one-dimensional motion of a particle. However, conservation of energy typically fails to specify the motion of a particle in more than one dimension. Adding conservation of angular momentum for two-dimensional motion in a central potential puts off the inevitable. But finally we must move beyond the powerful conservation of energy to the still more powerful principle of least action.
The comment that the principle of least action deals awkwardly with dissipative and frictional forces is certainly valid. Under our proposal, force is not eliminated but becomes a secondary concept, available to analyze friction and dissipative forces. Making force secondary clears center stage for the principle of least action to predict motions of a huge variety of simple and complex systems.
As pointed out by Thomas A. Moore, "Not only does the least-action principle offer a means of formulating classical mechanics that is more flexible and powerful than Newtonian mechanics, variations on the least-action principle have proved useful in general relativity theory, quantum field theory, and particle physics. As a result, this principle lies at the core of much of contemporary physics." 10
The twin paradox helps us to predict how a high speed free particle moves in flat space–time. The traveling twin streaks away to a distant star, returning to greet her stay-at-home sister, who has relaxed in an inertial frame between the events of departure and return. The two alternative journeys are most clearly described using a world line, a position versus time plot. When the twins meet at the end of the trip, the reading on the wristwatch of the stay-at-home twin (who follows the natural straight world line) is greater than the reading on the wristwatch of the round-trip twin. The aging between the events of departure and arrival is greater along the straight world line than along every nearby alternative world line between these two events. This example illustrates nature's command to the stone: Follow the world line of maximal aging!
The stone obeys the principle of maximal aging even in curved space–time (because a local inertial frame can be defined on every segment of the free-particle world line). General relativity calls the resulting world line a geodesic. In the vicinity of a time-independent structure such as a nonspinning or spinning star, neutron star, or black hole, a time-independent metric relates aging along a segment of world line to particle displacement in space and time coordinates along that segment. By employing the metric and the principle of maximal aging, students can explore big chunks of general relativity without tensors or the field equations.11
General relativity is general, so the stone follows the maximal-aging geodesic in everyday motions near the Earth. For low speeds and weak gravitational effects, however, the principle of maximal aging simplifies to the nonrelativistic principle of least action.12 Newtonian mechanics thus becomes a limiting case of relativistic mechanics (see Fig. 1). No pedagogical reason keeps students from a first immersion in general relativity in their second year of physics instruction.
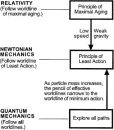 Figure 1.
Figure 1. Forms of the least action principle are useful not only in general relativity, but also in other contemporary fields of physics.10 Why not prepare our students to deploy this prodigious arsenal?
The least action command for the stone follows seamlessly (in the limiting case of large mass) from a conceptually simple approach to quantum mechanics devised by Feynman more than half a century ago.13 Nature's three-word command to the electron is Explore all paths! Here again path is understood to mean world line. Feynman's approach is well documented.14 In brief, Feynman tells us how to evaluate the contribution of each alternative world line to the probability that a particle emitted at event A will be detected at a later event B. The key point is that as the mass of a particle increases, the set of world lines between A and B that contribute significantly to the probability of detection at B shrinks to a narrow pencil around the world line of least action.15 In the limit of large mass this pencil contracts seamlessly to the single world line predicted by the principle of least action. Newtonian mechanics becomes an obvious special case of quantum mechanics (see Fig. 1). Using the Feynman approach, students can wield the power of quantum mechanics earlier in their careers than is possible when they start with the Schrödinger equation.
How far along are we in utilizing the principle of least action and its mighty siblings in the first and second year undergraduate physics curriculum? At least one introductory physics text, already in its second edition, begins Newtonian mechanics with the principle of least action.16 Another text, for honors students, introduces Lagrange's equations in an early chapter.17 These treatments provide existence proofs to guide us as we develop our own story line for the first year of undergraduate physics. At least one sophomore-level text explores general relativity using a variety of metrics together with the principle of maximal aging.11 The Feynman many-paths approach to quantum mechanics exists in scattered resources, some of them already used in classes.5
The principle of least action is simple, potent, and fundamental. It spans classical and contemporary physics and introduces deep concepts central to current research. Now is the time for action!
REFERENCES
Citation links [e.g., Phys. Rev. D 40, 2172 (1989)] go to online journal abstracts. Other links (see Reference Information) are available with your current login. Navigation of links may be more efficient using a second browser window.
-
Richard P. Feynman, The Feynman Lectures on Physics
(Addison–Wesley, Reading, MA, 1964), Vol. II, Chap. 19. Feynman writes
that "When I was in high school, my physics teacher—whose name was Mr.
Bader—called me down one day after physics class and said, `You look
bored; I want to tell you something interesting.' Then he told me
something that I found absolutely fascinating, and have, since then,
always found fascinating
 the principle of least action."
first citation in article
the principle of least action."
first citation in article
-
We use the phrase Newtonian mechanics to mean nonrelativistic,
nonquantum mechanics. Some texts use the term classical mechanics to
include both Newtonian and relativistic mechanics. first citation in article
-
An editorial is not the setting in which to discuss technical details
of these statements. See the mechanics texts in Ref. 6 and Herbert
Goldstein, Charles Poole, and John Safko, Classical Mechanics (Addison–Wesley, Reading, MA 2002), 3rd ed. For further background, see Ref. 5.
first citation in article
-
The action for an actual path may be a saddle point rather than a
minimum. So the most general, but rather esoteric, term for our basic
law is the principle of stationary action. first citation in article
-
Sample software and student materials for both general relativity and
quantum mechanics appropriate for the second year of study are
available at
 www.eftaylor.com/
www.eftaylor.com/ .
first citation in article
.
first citation in article
-
L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics (Butterworth-Heinenann, London, 1976), 3rd ed., Vol. 1, Chap. 1. Gerald Jay Sussman and Jack Wisdom, Structure and Interpretation of Classical Mechanics (MIT, Cambridge, 2001), Chap. 1.
first citation in article
-
Jozef Hanc, Edwin F. Taylor, and Slavomir Tuleja, "Deriving Lagrange's
equations using elementary calculus," Am. J. Phys. (submitted). See
also Cornelius Lanczos, The Variational Principles of Mechanics (Dover, New York, 1986), 4th ed., pp. 49–54.
first citation in article
-
Max Jammer, Concepts of Force (Dover, New York, 1999), preface.
first citation in article
-
Roger A. Hinrichs and Merlin Kleinbach, Energy: Its Use and the Environment (Harcourt Brace, New York, 2002), 3rd ed.;
Gordon Aubrecht, Energy (Prentice–Hall College Division, Englewood Cliffs, NJ, 1994), 2nd ed.;
Thomas A. Moore begins the study of mechanics with conservation laws in Six Ideas That Shaped Physics, Unit C: Conservation Laws Constrain Interactions (McGraw–Hill, New York, 2003), 2nd ed.
first citation in article
-
Thomas A. Moore in the entry on "least-action principle" in Macmillan Encyclopedia of Physics (Simon & Schuster Macmillan, New York, 1996), Vol. 2, pp. 840–842.
first citation in article
-
Edwin F. Taylor and John Archibald Wheeler, Exploring Black Holes: Introduction to General Relativity (Addison–Wesley Longman, Reading, MA, 2000).
first citation in article
-
A brief derivation is available at Ref. 5.
first citation in article
-
Freeman Dyson in Some Strangeness in the Proportion,
edited by Harry Woolf (Addison–Wesley, Reading, MA, 1980), p. 376,
writes that "Thirty-one years ago (1949), Dick Feynman told me about
his `sum over histories' version of quantum mechanics. `The electron
does anything it likes,' he said. `It just goes in any direction at any
speed, forward or backward in time, however it likes, and then you add
up the amplitudes and it gives you the wave-function.' I said to him,
`You're crazy.' But he wasn't." first citation in article
-
Some background references are available at Ref. 5.
first citation in article
-
R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (McGraw–Hill, New York, 1965), p. 29.
first citation in article
-
Jorge Dias de Deus, Mário Pimenta, Ana Noronha, Teresa Peña, and Pedro Brogueira, Introducción al la Física (Spanish) (McGraw–Hill, New York, 2001), ISBN 84-481-3190-8 and Introdução à Física (Portuguese) (McGraw–Hill, New York, 2000), 2nd ed., ISBN 972-773-035-3.
first citation in article
-
David Morin introduces Lagrange's equations in Chap. 5 of his honors introductory physics text. A draft is available at
 http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf
http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf .
first citation in article
.
first citation in article
CITING ARTICLES
This list contains links to other online articles that cite the article currently being viewed.
-
Action: Forcing Energy to Predict Motion
Dwight E. Neuenschwander et al., Phys. Teach. 44, 146 (2006)
-
Use of the Einstein–Brillouin–Keller action quantization
Lorenzo J. Curtis et al., Am. J. Phys. 72, 1521 (2004)
-
Getting the most action out of least action: A proposal
Thomas A. Moore, Am. J. Phys. 72, 522 (2004)
-
From conservation of energy to the principle of least action: A story line
Jozef Hanc et al., Am. J. Phys. 72, 514 (2004)
-
Modern mechanics
Ruth W. Chabay et al., Am. J. Phys. 72, 439 (2004)
FIGURES
 Full figure (22 kB)
Full figure (22 kB)Fig. 1. Story line showing the principle of least action sandwiched between relativity and quantum mechanics. First citation in article
Up: Issue Table of Contents
Go to: Previous Article | Next Article
Other formats: HTML (smaller files) | PDF (38 kB)
![[integral]](call_action_files/int.gif) L dt =
L dt = ![[integral]](call_action_files/int.gif) (T–V)dt, where T is the kinetic energy, V is the potential energy, and L is the Lagrangian (L = T–V in simple cases) along each segment of the path.3 The quantities T, V, L, and S are scalars. The principle of least action demands that the action S be a minimum for the path taken by the particle.4 For one-dimensional motion in a conservative potential, students can use interactive graphics software to seek out by trial and error the path that minimizes the action.5
(T–V)dt, where T is the kinetic energy, V is the potential energy, and L is the Lagrangian (L = T–V in simple cases) along each segment of the path.3 The quantities T, V, L, and S are scalars. The principle of least action demands that the action S be a minimum for the path taken by the particle.4 For one-dimensional motion in a conservative potential, students can use interactive graphics software to seek out by trial and error the path that minimizes the action.5 ![(<i>d</i>/<i>d</i><i>t</i>)((([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i>-dot)))–(([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i>)) = 0,](call_action_files/423_1m0.gif)
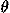 , and
, and 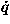 is the time derivative of q. Lagrange's scalar equations allow us to analyze with equal ease the motion of a particle or a system subject to constraints, such as a compound pendulum. In contrast, F = ma requires us to determine every single (vector!) force of constraint before we can describe the motion of even the simplest compound system. As stressed by Max Jammer, "
is the time derivative of q. Lagrange's scalar equations allow us to analyze with equal ease the motion of a particle or a system subject to constraints, such as a compound pendulum. In contrast, F = ma requires us to determine every single (vector!) force of constraint before we can describe the motion of even the simplest compound system. As stressed by Max Jammer, " modern particle physics, just like general relativity, seems to support the thesis that the concept of force has reached the end of its life-cycle—its disbarment from the inventory of fundamental concepts in physics
modern particle physics, just like general relativity, seems to support the thesis that the concept of force has reached the end of its life-cycle—its disbarment from the inventory of fundamental concepts in physics Figure 1.
Figure 1. 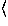 www.eftaylor.com/
www.eftaylor.com/ .
.